
힘과 모멘트, 바리뇽의 정리와 라미의 정리
건축구조역학은 물리적 개념을 바탕으로 한 이해가 필요한 부분이다. 역학의 기초가 되는 힘과 모멘트의 개념과 과학자, 수학자의 법칙 관련해서 학습할 필요가 있다. 비전공자라면 중학교 때 배운 수학, 과학의 기억을 끄집어내야 하며, 건축 구조는 공학 계산기로 계산을 해야 하는 문제가 있어 기사 시험에서 사용할 수 있는 계산기를 사전에 준비해야 한다.
1. 힘과 모멘트
힘 (Force, F 또는 P)
물체를 이동시키려하는 힘은 무게 단위로 N (Newton)을 사용함
영국 자연 철학자이자 물리학자, 아이작 뉴턴 (Isaac Newton, 1642~ 1726/27)
뉴턴의 운동의 법칙
- 제1 법칙, 관성의 법칙 : 정지한 물체는 계속 정지해 있고, 운동하는 물체는 계속 등속 직선운동을 한다는 법칙
- 제2 법칙, 가속도의 법칙: 물체에 힘 (F)이 작용하면 힘의 방향으로 가속도 (a)가 생기는데, 그 크기는 힘의 크기에 비례하며 질량 (m)에 반비례한다는 법칙
- 제3 법칙, 작용, 반작용의 법칙: A가 B에 힘 FA를 가할 때, B도 A에게 힘 FB를 가한다는 법칙
힘의 3요소

- 크기: 화살선의 길이로 표시
- 방향: 화살선의 기울기와 방향으로 표시
- 작용점: 화살 선상의 한 점으로 표시
힘의 방향과 부호
| 부호 | + | - |
| 수직 방향 (상 하) | ↑ 상 | ↓ 하 |
| 수평 방향 (좌 우) | → 우 | ← 좌 |
| 모멘트 방향 (시계 반시계) | ⤾ 시계 | ⤿ 반시계 |
모멘트 (Moment, M)
힘의 회전능력을 말하며, 어떤 점을 중심으로 회전하려는 크기를 모멘트라 함. 모멘트의 크기는 힘의 크기와 회전점으로부터 힘의 작용 선상의 최단거리의 곱으로 표시함.
모멘트(M)= 힘 (P) * 수직거리 (L)
우력 모멘트 (Couple Moment)

힘의 크기가 같고 방향이 반대인 한 쌍의 힘을 우력이라 하며, 우력에 의해서는 항상 모멘트가 발생하며, 우력 모멘트의 크기는 그 작용 위치와 관계없이 일정한 값을 가짐.
2. 작용점이 같은 두 힘의 합력 산정

합력은 힘을 합한 결과 (Resultant)라는 의미로 R 로 표시함
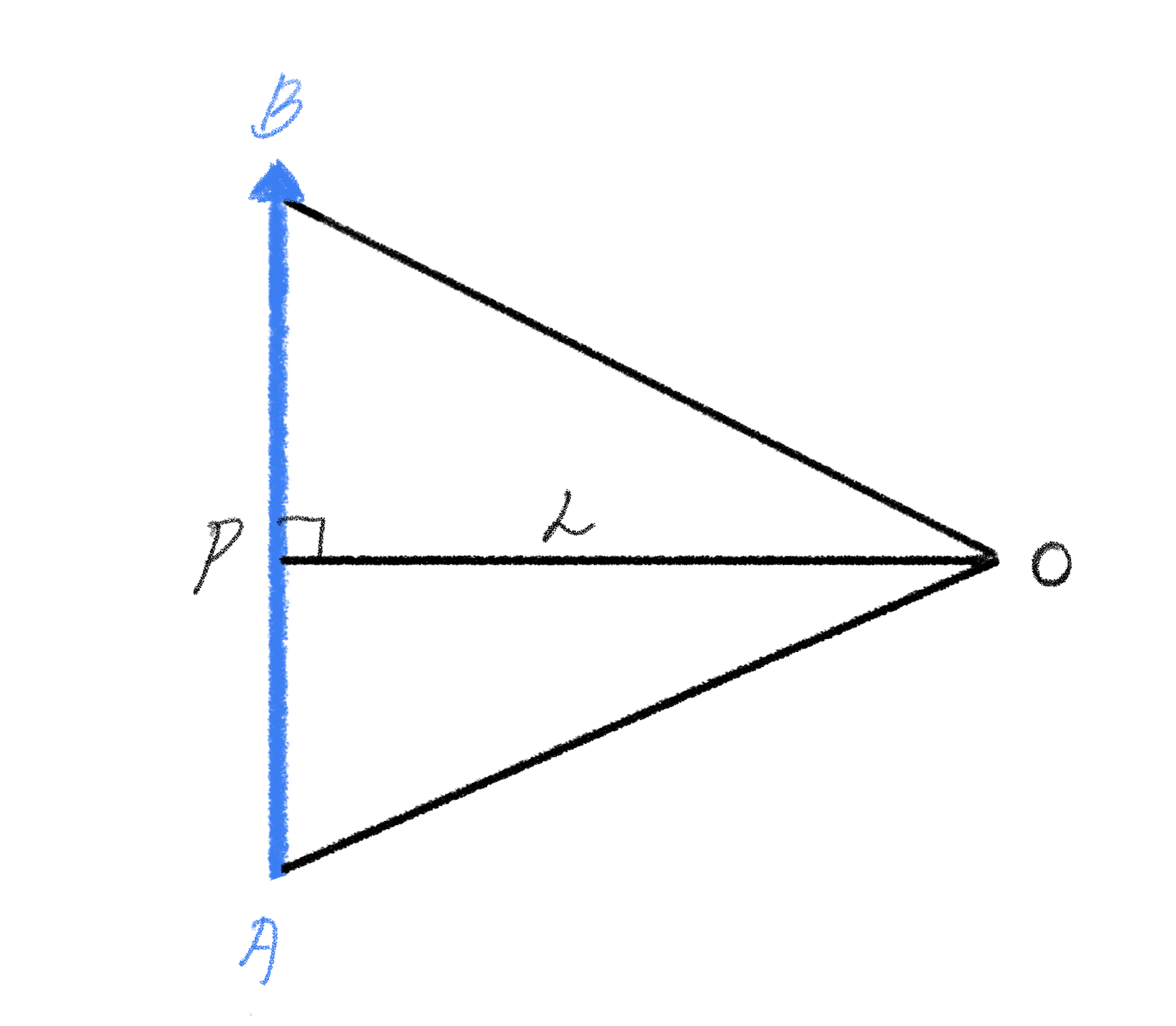
합력 (R): 직각삼각형 OCD에서 피타고라스의 정리 적용
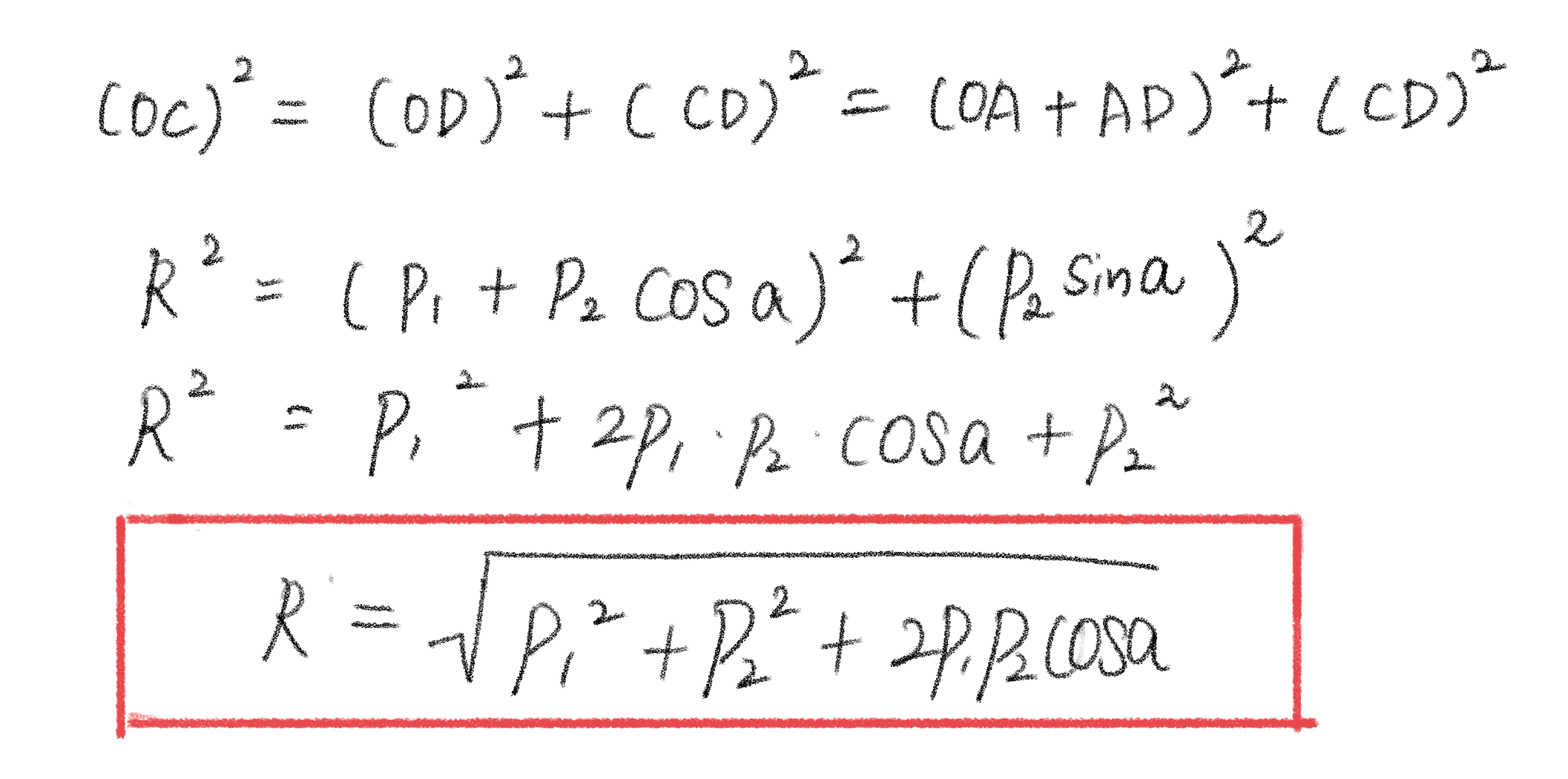
합력의 방향 (θ)

여기서 잠깐!
피타고라스 정리와 삼각비를 다시 정리

3. 바리뇽의 정리 (Varignon's Theorem)
프랑스 수학자, 피에르 바리뇽 (Pierre Varignon, 1654~1722)
Pierre Varignon - Wikipedia
French mathematician Pierre VarignonBorn1654Died23 December 1722NationalityFrenchKnown forstatics, mechanics, infinitesimal calculus, convergence of series, water clock, mechanical explanation of gravitation, Varignon's theoremScientific careerFieldsMathe
en.wikipedia.org
나란한 여러 힘이 작용할 때 임의의 한 점에 대한 모멘트의 합은 그 점에 대한 합력(Resultant)의 모멘트와 같다.
즉, 분력의 모멘트의 합은 합력의 모멘트와 같다.

적용
나란한 힘들은 각 힘의 작용점이 서로 다름, 따라서 이들 나란한 힘의 합력의 작용 위치(x)를 구할 때 바리뇽의 정리가 사용하며
이동 하중에 대한 보의 절대 최대 휨 모멘트(Mabs, Max) 산정 및 RC 구조에서 기둥 부재의 소성 중심 (Plastic Centroid)를 구하는 데 응용할 수 있다.
예제) 그림에서의 같은 평행력에 있어서 P1, P2, P3, P4의 합력의 위치는 O 점에서 얼마의 거리에 있는가?
풀이) 나란히 여러 힘의 합력을 구한다.
-8-4+6-10 = -16kN
O점에 대하여 합력의 작용 위치 x를 구하면
R*x = P1*x1 + P2*x2 + P3*x3 + P4*x4
-16*x = -8*9 + 4*7+6*4-10*2
x = 6m

4. Sin 법칙
중학교 2학년 수학에 나오는 법칙이라는데 기억이 나질 않는다.

삼각형에서 한 변의 길이와 내각의 Sin값은 비례한다.
5. 라미의 정리 (Lami's Theorem)
프랑스 수학자, 베르나르 라미 (Bernard Lamy, 1640 ~ 1715)
Bernard Lamy - Wikipedia
Bernard Lamy (15 June 1640, in Le Mans, France–29 January 1715, in Rouen, France) was a French Oratorian, mathematician and theologian. After studying in Le Mans, he went to join the Maison d'Institution in Paris, and to Saumur thereafter. In 1658 he ent
en.wikipedia.org
수학의 Sin 법칙을 공학 분야에서 실용화 시킨 것이 라미의 정리로 세 힘이 서로 평형 상태에 있을 때 이들 세 힘은 동일 평면 상에 있고 한 점에서 만난다.

한 점에 미치는 두 힘의 크기가 같고 방향이 반대이면 세 힘은 항상 평형 상태가 된다.
예제 ) 그림과 같은 로프에서 BC에 발생하는 힘의 크기는 얼마인가? (단, 인장: +, 압축: - )
풀이) Fbc/ sin150˚ = 10kN/sin90˚
Fbc = +5kN (인장)


