
구조물은 평형상태를 유지하고 있으므로 구조물을 해석하는 데 있어 평형에 대한 이해가 선행되어야 하며 안정한 구조물의 정정과 부정정 상태를 구할 수 있어야 한다.
1. 구조물 평형
구조물에 작용하는 하중에 의해 구조물이 평형상태를 유지하기 위해서는 구조물이 이동하지 않고 회전하지도 않는 안정 (stable) 상태를 말한다.
| 조 건 | 수평력 평형 | 수직력 평형 | 회전력 평형 |
| 내 용 | 수평으로 작용하는 하중에 의하여 지점에서는 수평방향의 반력이 발생하여 구조물 좌 우로 움직임이 없어야 함 | 수직으로 작용하는 하중에 의하여 지점에서는 수직방향의 반력이 작용하여 상, 하로 움직이지 않음 | 회전력 (모멘트 하중)에 의하여 지점에서는 모멘트 반력이 발생하여 회전하지 않아야 함 |
| 그 림 |  |
 |
 |
| 평형 조건식 | ∑H = 0 | ∑ V= 0 | ∑ M = 0 |
2. 힘의 방향과 부호
[건축기사] 건축구조_힘과 모멘트, 바리뇽의 정리와 라미의 정리 참조
[건축기사] 건축구조_힘과 모멘트, 바리뇽의 정리와 라미의 정리
건축구조역학은 물리적 개념을 바탕으로 한 이해가 필요한 부분이다. 역학의 기초가 되는 힘과 모멘트의 개념과 과학자, 수학자의 법칙 관련해서 학습할 필요가 있다. 비전공자라면 중학교 때
ex-nihil0.com
3. 구조물 판별
3-1. 안정과 불안정
- 안정: 외력이 작용했을 때 구조물이 항상 평형을 이루는 상태 (위치나 모양의 변화가 없음)
- 불안정: 외력이 작용했을 때 구조물이 평형을 이루지
못하는상태 (위치나 모양이 변화함) N ≤ -1
3-2. 정정과 부정정
- 정정: 안정한 구조물이며, 힘의 평형조건식으로 반력과 부재력을 구할 수 있는 상태, 최소한도의 안정, N=0
- 부정정: 안전한 구조물이며, 힘 평형조건식으로만 반력과 부재력을 구할 수
없는상태, 건축 구조물은 부정정 구조를 갖도록 함. N≥ +1
4. 구조물의 지점 (Support) 과 절점 (Joint)
| 구 분 | 지점 상태 | 표시법 | 지점반력 (Reaction) |
| 이동 지점 | 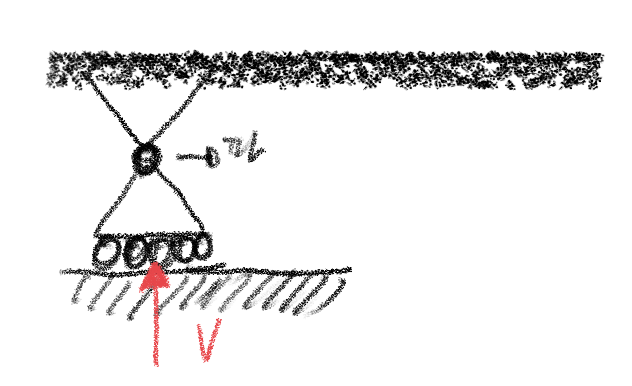 |
 |
1개 (V) |
| 회전 지점 |  |
 |
2개 (V, H) |
| 고정 지점 |  |
 |
3개 (V, H, M) |
| 회전절점 (Hinged Joint, 활절점) | 고정절점 (Fixed Joint, 강절점) |
 |
 |
| 부재와 부재의 절점이 핀 (Pin)으로 연결되어 회전이 강한 상태, | 부재와 부재의 절점이 고정되어 각도가 변하지 않는 상태 |
4-1. 구조물의 결합: 구조물에 관통하는 절점, h = -1
 |
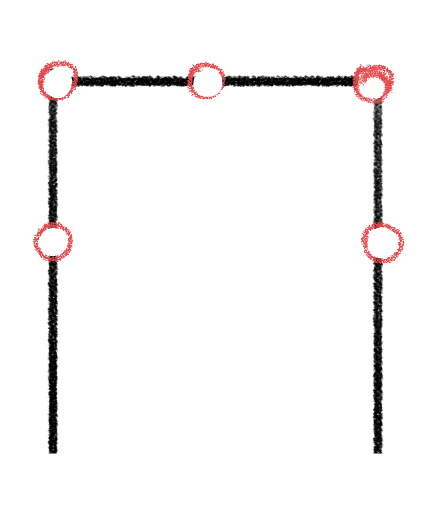 |
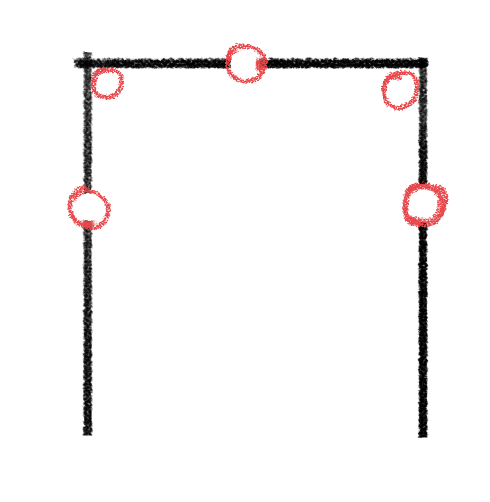 |
| h= 0 | h= -5 | h= -3 |
5. 구조물의 수평 대각 보강
 |
 |
 |
 |
 |
 |
6. 보 · 라멘의 부정정 차수
부정정 차수 (N) = 외적 차수 (Ne) * 내적차수 (Ni)
외적차수 Ne = r (지점 반력수) - 3
내적차수 Ni = h (Hinged, 부재 내의 힌지 절점수) + 연결 부재에 따른 차수
6-1. 보 (Beam)의 부정정 차수 계산 예시
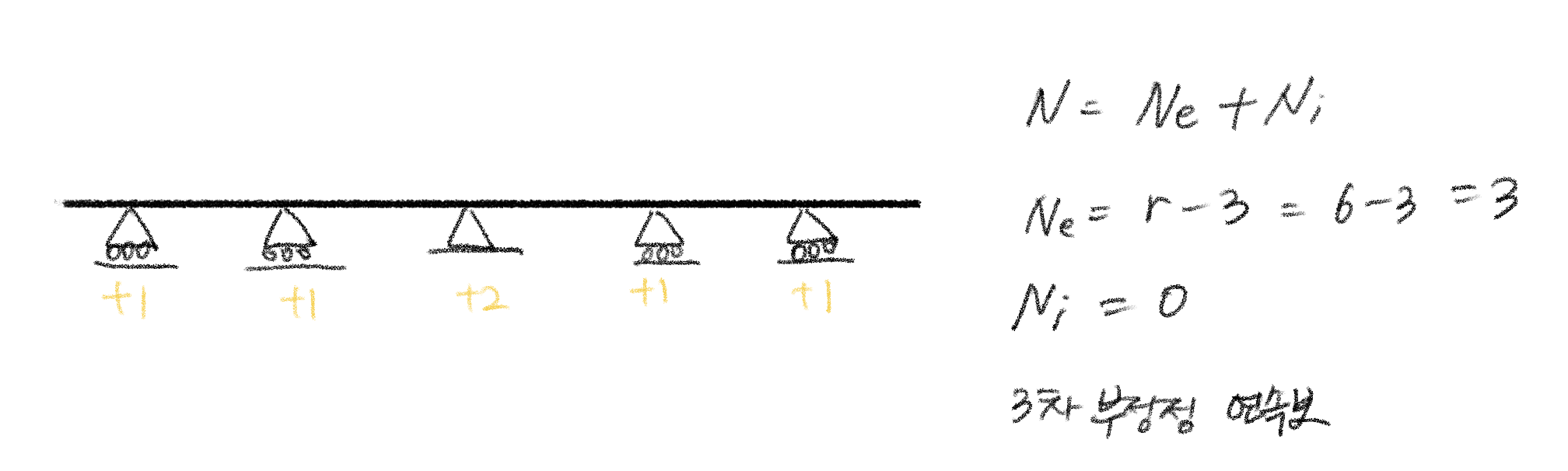
6-2. 라멘 (Rahmen)의 부정정 차수 계산 예시

7. 트러스 (Truss)의 부정정 차수

트러스 구조는 부재(member)가 삼각형 단위로 구성된 구조형식으로 절점 (Joint)은 기본적으로 힌지 (Hinge)로 가정하는 구조형식. 즉, 3개의 부재내력 중 전단력 (Shear Force)와 휨 모멘트 (Bending Moment)가 발생하지 않고 축방향력 (Axial Force)만 발생하는 구조형식으로 삼각형이 계속 만들어진다면 내적차수는 0이 됨.
부정정 차수 (N) = 외적 차수 (Ne) * 내적차수 (Ni)
트러스 부정정 차수 간편식
N = r + m -2j
r: 지점 반력 수
m: + 1 연결 부재의 개수
j: 절점의 개수

8. 형태 불안정 구조
부정정 차수를 계산하면 0이 계산되지만 구조물의 지점 이동 및 과도한 절점 변형을 수반하는 대표적인 형태불안정 구조들이 있다.
이러한 형태 불안정 구조들은 정정으로 계산되어 안정이라고 생각하기 쉽지만 외적인 하중이 작용했을 때는 불안정 구조가 된다.


